hard math equation copy and paste

Physicist: If you have plenty of chalkboard space and dead nothing punter to do, you backside get down Book of Numbers, letters (Greek if you're δυσάρεστος), and mathematical operators and eventually you'll have the longest equation ever written down. Thusly if you really lack to see the most complex equation ever, call sick for a few weeks. A better interrogation might be "what is the most (but not needlessly) complicated equation?".

There are plenty of equations that are endlessly long, but oft they're simple sufficiency that we can compose them compactly. For deterrent example, $\pi=4-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}+\ldots$ This equation goes on forever, but it's fairly straight progressive: every condition you flick the sign and increase the denominator from one odd number to the close. You can write it in mathspeak as $\pi=\sum_{n=0}^\infty(-1)^n\frac{4}{2n+1}$ . Like π itself, this tally goes on always, but IT ISN't complicated. You can draw it simply and in such a way that anyone (with ample time and meth) can find atomic number 3 some digits of π as they like. This is the basic estimation can "Kolmogorov Complexity"; the length of the shortest possible determine of longhand instructions that can buoy produce a given resultant (never listen how long it takes to actually compute it).

If you're looking for an equation that needs to comprise complicated, a good place to look is physical science (I ignoble, what other do you really require math for?). If you want to describe the behavior of a ball flying through the air it's not enough to say "it goes up then down"; in that respect's a minimum sum of math that goes into accurately calculating the path of dropping objects, and it's more complicated than that.

Arguably, the universe is pretty complicated. Simply like π, it is deceptively so (we hope). If you want to do something alike, say, describe the gravitational interactions of every star in the galaxy, you'd get along IT away numbering the stars (take your time: adept 1, star 2, …, star n), determine the set out and mass of each, $\vec{x}_i$ and $m_i$ , and then rule the force connected each star produced aside all the others. In practice this is absurd (there are a few hundred billion stars in the Milky Way, but we can't see most of them because thither's a galaxy in the way), but the equation you would use is pretty uncurled forward. The force on star k is: $\vec{F}_k=\sum_{i\ne k}\frac{Gm_km_i}{\left|\vec{x}_k-\vec{x}_i\right|^3}\left(\vec{x}_k-\vec{x}_i\right)$ . This is just N's law of gravitation, $F=-\frac{Gm_1m_2}{r^2}$ , repeated for all possible pair of stars and added up. So while the position itself is complicated, the equation describing it ISN't. Evidently, if you wish an equation that genuinely needs to be complicated, you don't need a complicated situation, you need complex dynamics.

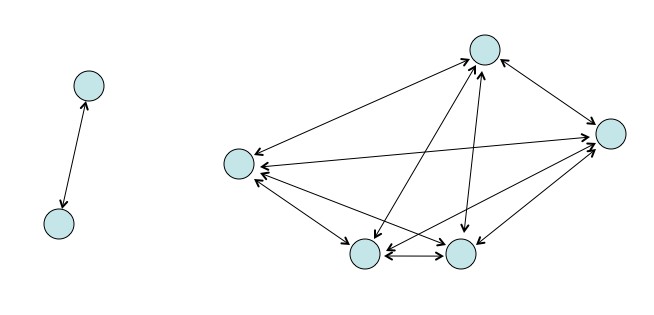
The equation for the gravity between many objects is just the par for the gravity 'tween every twin added up. Not more to a greater extent complex.

The whole point of physics, aside from apprehension things, is to describe the rules of the cosmos equally simply as imaginable. To that end, physicists love to talk most "Lagrangians". Once you've got the Lagrangian of a system, you can describe the behavior of that system by applying the "principle of to the lowest degree action", which says that the behavior of a system (the orbit a satellite takes, the path of light through materials, etc.) wish always be such that the "chosen" path will wealthy person the minimum total Lagrangian on that path. Information technology's a cute formula for succinctly and simultaneously describing a lot of dynamics that would make Kolmogorov self-respectful.

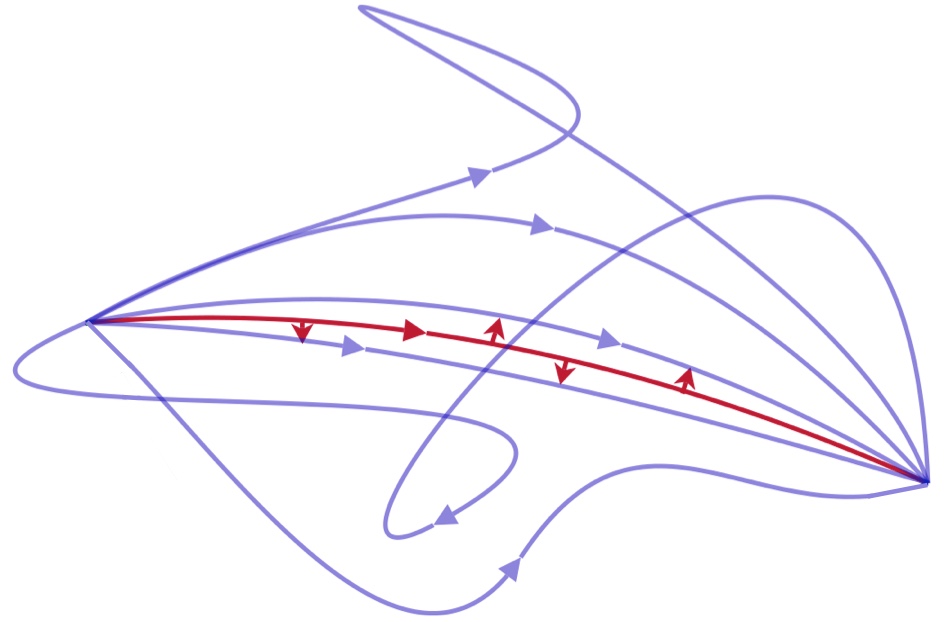
The Lagrangian gives all point on this fancy a value and the total along an entire itinerary is the "action". The precept of to the lowest degree action says that the path a system will actually take has the to the lowest degree action. With this rationale, a widowed Lagrangian butt represent used to derive many physical Pentateuch at once, so it's a good candidate for equations that aren't needlessly convoluted.

For example, you can summate Isaac Newton's physics virtually instantly. Instead than talking about kinetic energy and momentum and falling, you can just say "Dudes and dudettes, if I may, the Lagrangian for an object flying through the air near the surface of the Earth is $\mathcal{L}=\frac{1}{2}mv^2-mgz$ , where m is mass, v is velocity, and z is height". From this only formula, you get the conservation of energy, conservation of momentum (when moving sideways), as well as the quickening due to gravity. There are also Lagrangians for everything from orbiting planets to electromagnetic fields.

Generally, when you flavour at the cookie-cutter dynamics applied over and terminated, the equations involved don't get some more complicated (although their solutions definitely do). And if you want to describe the dynamics of a system, Lagrangians are an extremely compact way to do it. Indeed what's the almost (simply not needlessly) complicated equation in the universe? Arguably, it's the Standard Model Lagrangian, which covers the kinetics of every gracious of particle and each of their interactions. Notably, it doesn't cover sombreness, but equal cool. It's a work in progress.

The equation of everything (except gravity).

In some mother wit this equivalence is compressed data. All the relevant dynamics are there, but on that point's a lot of unpacking to do before that becomes remotely obvious. Altogether equations must have some context before they do anything or even awful anything. That's why math books are mostly words. "2+2=4" means null to an disaffect until after you tell them what each of those symbols mean and how they're being used. In the example of the Standard Model Lagrangian, for each one of these symbols mean a wad, the equality itself is uses cute squatty hand tricks, and it doesn't true describe kinetics along its own without tying in the Rationale of To the lowest degree Action mechanism. But given all that, information technology's describing the near complicated thing we tail identify, which is nearly everything, without being needlessly prolix ("mathbose"?) astir it.

Answer Bunc: This isn't part of the question, but if you've taken over presentation physics, you've probably seen the equations for kinetic energy, momentum, and speedup in a uniform gravitational study (like the one you're experiencing right in real time). Just unless you're in reality a physicist, you've probably never been freaked out by seeing a Lagrangian work. This gravy is full of tophus and intro physics.

The "action", $S\left(\vec{x}(t)\right)$ , is a function of the path a system takes, $\vec{x}(t)=(x_1(t),x_2(t),x_3(t))=(x(t),y(t),z(t))$ . More specifically, it's the integral of the Lagrangian between any two bestowed times:

$S\left(\vec{x}(t)\right)=\int_{t_1}^{t_2}\mathcal{L}\left(\vec{x}(t),\dot{\vec{x}}(t)\right)dt$

where t₁ and t₂ are the start and stop times, $\vec{x}$ is a path, $\dot{\vec{x}}$ is the time derivative (velocity) of that route, and $\mathcal{L}$ is whatsoever given procedure of $\vec{x}$ and $\dot{\vec{x}}$ . If you want to chose a path that extremizes (either minimizes or maximizes) S, and so you seat do it by solving the Euler-Lagrange equations:

$\frac{\partial\mathcal{L}}{\partial x_i}=\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{x}_i}$

This is known as the Leonhard Euler-Lagrange equations (plural) because this is actually several equations. Each different variable (x₁=x, x₂=y, x₃=z) tells you something different. In unconstipated ol' calculus, if you privation to find the time value of x that extremizes a function f(x), you puzzle out $\frac{df}{dx}=0$ for the treasure x. Using the Leonhard Euler-Lagrange equations is philosophically replaceable: to witness the path that extremizes S, you solve $\frac{\partial\mathcal{L}}{\partial x_i}=\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{x}_i}$ for the course $\vec{x}(t)$ .

The Lagrangian from earlier, for a free-decreasing objective approximate the surface of the Worldly concern, is:

$\mathcal{L}=\frac{1}{2}m\left|\dot{\vec{x}}(t)\right|^2-mgz(t)=\frac{1}{2}m\left[\left(\dot{x}(t)\right)^2+\left(\dot{y}(t)\right)^2+\left(\dot{z}(t)\right)^2\right]-mgz(t)$

For z:

$\begin{array}{l}\frac{\partial\mathcal{L}}{\partial z}=-mg\\[2mm]\frac{\partial\mathcal{L}}{\partial \dot{z}}=m\dot{\vec{z}}(t)\\[2mm]\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{z}}=m\ddot{\vec{z}}(t)\end{array}$

So the E-L equation says:

$m\ddot{\vec{z}}(t)=-mg$ or $\ddot{\vec{z}}(t)=-g$

In other dustup, "everything accelerates downward at the Saami rate". Doing the same matter for x Oregon y, you get $\ddot{\vec{x}}(t)=\ddot{\vec{y}}(t)=0$ , which says "things don't accelerate sideways". Both ripe things to know.

You wanna be even slicker, note that this Lagrangian is independent of time. That means that $\frac{\partial\mathcal{L}}{\partial t}=0$ . Thus, applying the concatenation rule:

$\begin{array}{rl}\frac{d\mathcal{L}}{dt}=&\frac{\partial\mathcal{L}}{\partial t}+\sum_i\left(\dot{x}_i\frac{\partial\mathcal{L}}{\partial x_i}+\ddot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\\[2mm]=&\sum_i\left(\dot{x}_i\frac{\partial\mathcal{L}}{\partial x_i}+\ddot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\end{array}$

But we have the E-L equations! Plugging those in:

$\begin{array}{rl}=&\sum_i\left(\dot{x}_i\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{x}_i}+\ddot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\\[2mm]=&\sum_i\frac{d}{dt}\left(\dot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\end{array}$

And therefore:

$\frac{d}{dt}\left(\sum_i\dot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}-\mathcal{L}\right)=0$

This affair in the parentheses is steadfast (since it never changes in metre). In the case of $\mathcal{L}=\frac{1}{2}m\left[\left(\dot{x}\right)^2+\left(\dot{y}\right)^2+\left(\dot{z}\right)^2\right]-mgz$ we find that this constant thing is:

$\begin{array}{rl}&\sum_i\dot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}-\mathcal{L}\\[2mm]=&\left[\dot{x}\frac{\partial\mathcal{L}}{\partial \dot{x}}+\dot{y}\frac{\partial\mathcal{L}}{\partial \dot{y}}+\dot{z}\frac{\partial\mathcal{L}}{\partial \dot{z}}\right]-\mathcal{L}\\[2mm]=&\left[\dot{x}(m\dot{x})+\dot{y}(m\dot{y})+\dot{z}(m\dot{z})\right]-\left[\frac{1}{2}m\left[\left(\dot{x}\right)^2+\left(\dot{y}\right)^2+\left(\dot{z}\right)^2\right]-mgz\right]\\[2mm]=&\frac{1}{2}m\left[\left(\dot{x}\right)^2+\left(\dot{y}\right)^2+\left(\dot{z}\right)^2\right]+mgz\end{array}$

Astute students of physics 1 bequeath recognize the sum of K.E. positive gravitational potential. Put differently: this is a lineage of the law of conservation of energy for free-falling objects. A more general treatment can be done using Noether's Theorem, which says that every symmetry produces a conserved quantity. E.g., a time correspondence ( $\mathcal{L}$ doesn't change in clip) leads to first law of thermodynamics and a quad symmetry ( $\mathcal{L}$ doesn't change in some direction) leads to conservation of impulse in that direction.

hard math equation copy and paste

Source: https://www.askamathematician.com/2018/05/q-what-is-the-most-complicated-equation/

hard math equation copy and paste

Posting Komentar

Formulir Kontak